My balsa sheet balanced at 2 1/4″ = 2.25″.  Dividing that into 30.0 gives us a weight of 13.3 grams.  This is a 1/16″ x 3″ x 36″ piece of wood.  We can calculate the density of the wood, usually rated in pounds per cubic foot.  13.3 grams divided by 28.35 grams per ounce divided by 16 ounces per pound is 0.0294 pounds.  1/16″ x 3″ x 36″ is 6.75 cubic inches, divided by 12 x 12 x 12 = 1,728 cubic inches per cubic foot makes it 0.00391 cubic foot.  Dividing the weight by the volume gives a density of 7.52 pounds per cubic foot, so this would be classed as 7# wood.   You can use this as a guide when buying balsa sheet, the ratio of a 1/16″ x 3″ x 36″ sheet weight to the desired density is 13.3/7.52 = 1.77.  If you want 5# wood, look for a sheet weighing 5 x 1.77 = 8.84 grams.  This would balance 3.39″ = 3 3/8″ out on the described scale.

My yellow tissue paper balanced at 3 7/16″ = 3.4375″, dividing that into 30.00 makes the weight 8.72 grams.  The two sheets of 20″ x 26″ have 2 x 20″ x 26″ = 1,040 square inches of area.  The area density of this tissue is thus 8.72 grams per 1,040 square inches, or 0.839 grams per 100 square inches, 1.21 grams per square foot, 13.0 grams per square meter, 10.9 grams per square yard or 0.383 ounces per square yard.  there are many tables of density for model airplane covering and unfortunately there are many different units used.

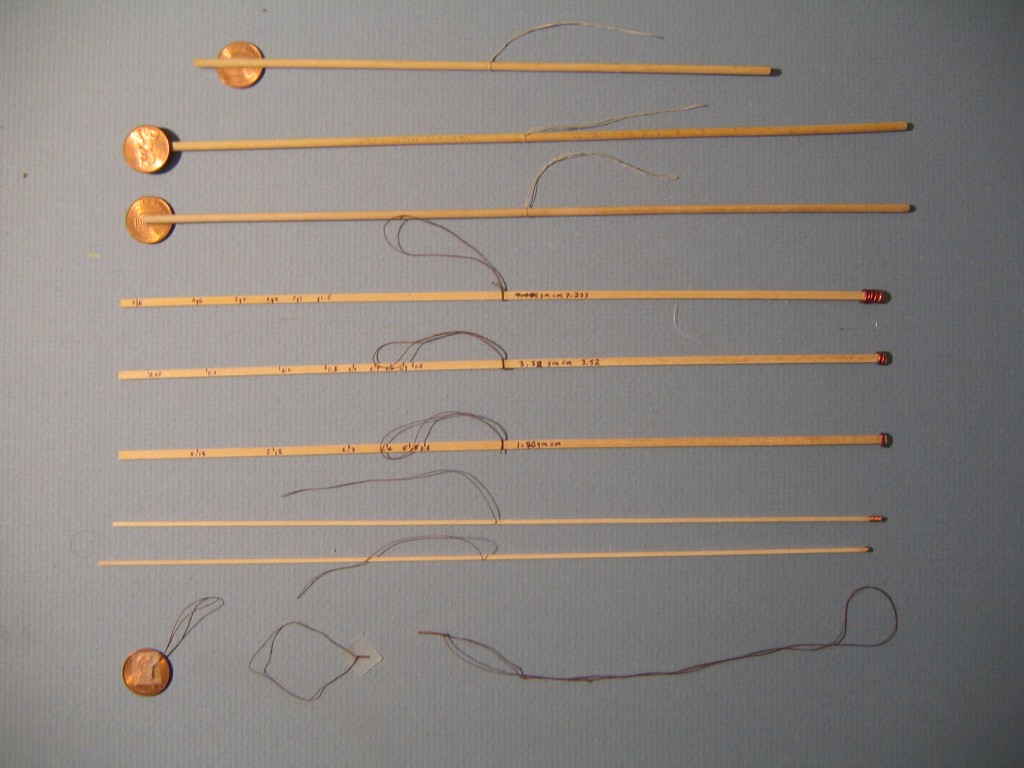
I made some penny balances using 1/8″ birch dowel.  I have used them to weigh the parts of my second Big Pussycat and get results just as good as my decigram triple beam balance, maybe better.  The first was 9″ long, four could be cut from a 36″ dowel.  I shaved about 1/3 of the width off 1 1/8″ of one end, making a flat place.  I tied a 2″ loop of thread around the center with a Larks Head knot, adjusted the position until the stick balanced horizontally, then glued it in place.  I glued a new penny to the flat place so its center was 10 cm from the fulcrum thread loop.  A post 1981 penny is 3/4″ in diameter, 3/8″ radius, and weighs 2.5 grams.  I taped another penny to a loop of thread and hung it 10 cm on the other side of the center mark, verifying that it balanced.  This has an unbalanced moment of 2.5 gm x 10 cm = 25 gm cm.  I calculated the distances for weights from 2.5 to 10 gm in 0.5 gm steps and marked them on the stick.  This one worked well for weighing the Big Pussycat; 3.60 gm for the airframe, 3.16 gm for the prop/noseblock assembly and 1.18 gm for the landing gear for a total weight of 7.94 grams .  The parts were taped to a thread loop, the thread was slid along the stick until it balanced, and the distance to the fulcrum measured in centimeters, to the nearest mm.  Weight is calculated as 25 gm cm moment divided by the distance in cm.  The cm scale reading is good to two significant figures with the third reasonably guesstimated.

 Here we find the prop assembly balances 7.90 centimeters from the fulcrum against a 2.50 gram penny at 10.0 centimeters from the fulcrum.  The products of the weights and distances on each side must be equal.  If the weight of the prop assembly is w, then 7.90 x w = 10.0 x 2.50 = 25.0, therefore w = 25.0/7.90 = 3.16 grams.

I find that the useful weight range is a ratio of about 5 to 1.  I have a set of lab weights to use for calibration.  All of these balances together will cost a lot less than the decigram lab balance I bought years ago and give results just as good or better.

I made another from 12″ of dowel with two pennies centered 15 cm from the center, but calibrated it in density units for 1/16″ x 3″ x 36″ balsa sheet, to use in the store for selecting 1/16″ balsa sheet. Using a 12″ length of 1/8″ dowel, file or sand flat places on opposite sides of one end for about 9/16″ from the end.  Or use a 12″ piece of 1/8″ square hard balsa or other wood.  Place the hanging loop of thread at the center of gravity of the stick, so it balances horizontally when hung there, and glue it in place.  Glue two shiny new pennies to the flat faces at the end so the center of the pennies is exactly 15 cm from the thread loop.  Pennies are exactly 0.75″ = 3/4″ in diameter, so the edge is 3/8″ from the center of the penny. New pennies minted after 1981 weigh 2.50 grams each.  The balance now has an unbalanced moment of 2 x 2.5 x 15 = 75 gram centimeters.  For a weight w grams to balance this at distance d centimeters on the other side of the stick, w x d must equal 75 gram centimeters.  You can tape a loop of thread to a balsa sheet, slide the loop along the stick until it balances, read the distance off with a centimeter scale, and calculate the weight from w = 75/d.  The scale can be calibrated directly in grams, or, for standard 1/16″ x 3″ x 36″ sheets of balsa, it can be calibrated directly in density units.  For the Big Pussycat you would look for wood with density between 6# and 8#. This table shows the densities in pounds per cubic foot, the corresponding weight of a 1/16″ x 3″ x 36″ sheet and the corresponding distance d.  Centimeter scales are usually divided into tenths (mm or millimeters) and you can eyeball the hundredth reasonably closely.  Mark these distances on your balance and write the densities down next to the marks.  You will note that the marks get closer together as the density goes up.  A balance for selecting 1/32″ sheet can be made in exactly the same way, but using a single penny.

Density  Weight  Distance

#          w gm        d cm

 3         5.32      14.11

 4         7.08      10.58

 5         8.86       8.47

 6       10.6         7.05

 7       12.4         6.05

 8       14.2         5.29

 9       16.0         4.70

10       17.7        4.23

11       19.5        3.85

12       21.3        3.55

13       23.0        3.26

14       24.8        3.02

15       26.6        2.82

20       35.4        2.12

22       39.0        1.92

24       42.5        1.76

I have made several more balances for measuring in different weight ranges.

Rather than use pennies as counterbalance weights, these use lengths of copper wire wrapped and glued to the stick.  By weighing a long piece of wire, the weight per unit of length may be calculated.  From that, a length having any desired weight may be cut.  That weight will be the minimum your balance can weigh.  It is not practical to weigh anything more than about five times that weight.  Each of these balances was calibrated with standard weights.  For example, the top wire wound balance was designed to weigh from 0.5 gram to 2.5 grams.  It uses a 1/16″ x 1/8″ x 12″ basswood stick.  The loop of thread was located so the stick itself balances perfectly, and the thread was glued in place.  It needs 0.5 grams of wire.  The appropriate length of wire was cut, wrapped around the stick and glued in place.  A short loop of thread was taped to a penny and slid along the stick until it balanced.  The distance from the fulcrum was 2.94 centimeters.  The product of the weight and distance is 2.50 x 2.94 = 7.35 gram-centimeters.  This is the moment of the wire weight.  You don’t need to know the exact weight or position of the balance weight, because the 7.35 is the only number you need.  Now you can measure the distance d to the point where any object of unknown weight w balances and calculate its weight as w = 7.35/d.  That coefficient is written right on the stick.  The thinnest balances were calibrated with short loops of wire.

Gary